题目大意.

给你一个排列 $a$$a$，你要把它变成排列 $b$$b$。你可以进行的是如下操作：【交换区间 $[l,r]$$[l,r]$ 内的最大值和最小值】。请在 $3\times {10}^5$$3\times10^5$ 步内完成这个目标。

$n\le 4000$$n\le 4000$。

由于操作是可逆的，我们可以把目标看作是要在 $1.5\times {10}^5$$1.5\times10^5$ 次操作内将一个特定排列排成 $1\sim n$$1\sim n$。

枚举排序算法（？），现在让我们考虑一下归并排序。

假设原序列的前一半和后一半已经有序，那么如何归并？

key observation：我们可以反转一个有序序列。借由此，我们可以合并两个值域不交且内部有序的序列。

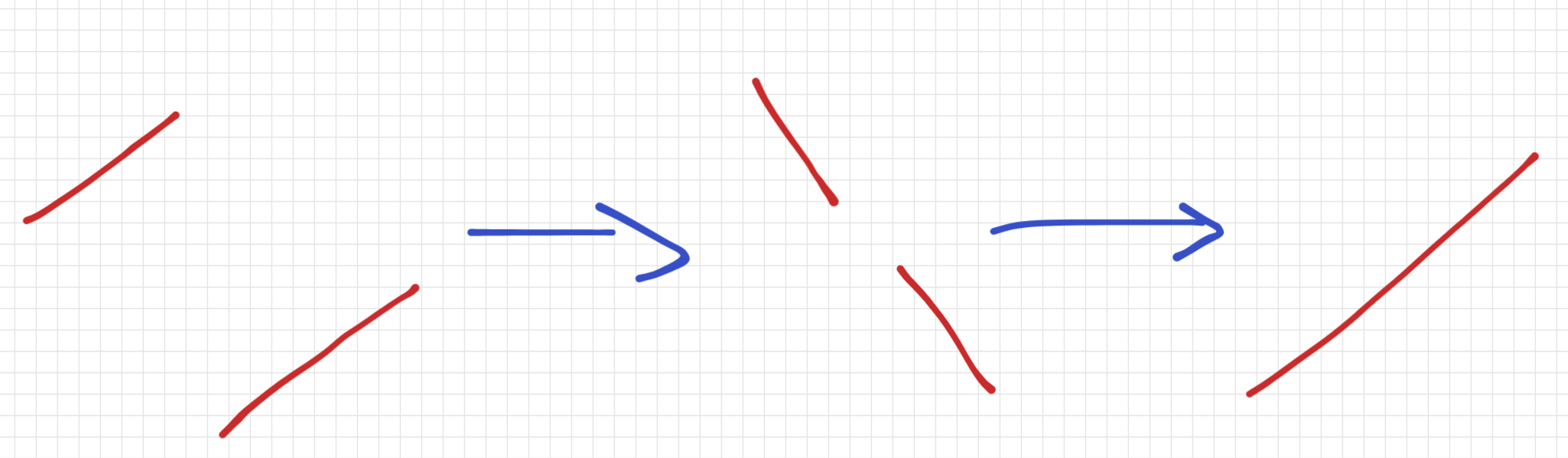
所以我们可以继续按值域分治：

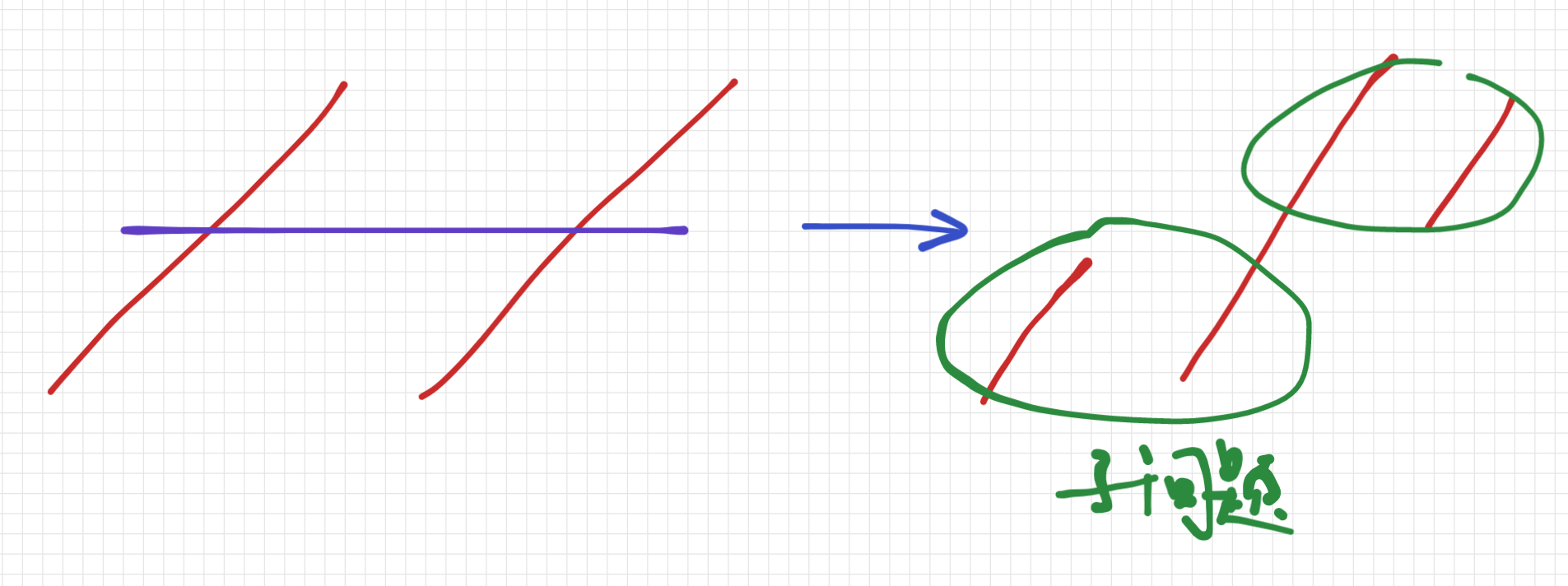
（请注意，紫线应使得子问题大小（$\le X$$\color{purple}\le X$ 的元素个数、$>X$$\color{purple}> X$ 的元素个数）尽量均衡。）

时间复杂度 $O(n{\log }^{2}n)$$O(n\log^2n)$。

​x
#include<bits/stdc++.h>
using namespace std;

const int maxn = 4100;

struct SOLVER {
    int A[maxn];
    vector<pair<int, int> > ans;
    void SWAP(int i, int j) {
        ans.emplace_back(i, j);
        swap(A[i], A[j]);
    }
    void REV(int l, int r) {
        while (l < r) SWAP(l, r), l++, r--;
    }
    void merge0(int l, int mid, int r) {
        if (l > mid || mid + 1 > r) return;
        REV(l, mid); REV(mid + 1, r); REV(l, r);
    }
    void merge(int l, int mid, int r) {
        if (l > mid || mid + 1 > r) return;
        int qaq = mid - l + 1;
        int i1 = l, i2 = mid + 1;
        for (int i = 1; i <= qaq; ++i) {
            if (i1 > mid) { i2++; continue; }
            if (i2 > r) { i1++; continue; }
            if (A[i1] < A[i2]) { i1++; continue; }
            if (A[i1] > A[i2]) { i2++; continue; }
        }
        merge0(i1, mid, i2 - 1);
        merge(l, i1 - 1, mid);
        merge(mid + 1, i2 - 1, r);
    }
    void SORT(int l, int r) {
        if (l == r) return;
        int mid = (l + r) >> 1;
        SORT(l, mid);
        SORT(mid + 1, r);
        merge(l, mid, r);
    }
} solA, solB;

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &solA.A[i]);
    solA.SORT(1, n);
    for (int i = 1; i <= n; i++) assert(solA.A[i] == i);
    for (int i = 1; i <= n; i++) scanf("%d", &solB.A[i]);
    solB.SORT(1, n);
    for (int i = 1; i <= n; i++) assert(solB.A[i] == i);

    reverse(solB.ans.begin(), solB.ans.end());
    printf("%d\n", solA.ans.size() + solB.ans.size());
    for (auto u : solA.ans) printf("%d %d\n", u.first, u.second);
    for (auto u : solB.ans) printf("%d %d\n", u.first, u.second);
}