贺了一遍题解/kk

题目大意.

你手上有一个二进制数 $x$$x$，这个数会经历若干次以下操作

• 对于每一位，有 $p_i$$p_i$​ 的概率不变，有 $(1-p_i)q$$(1-p_i)q$​ 的概率变为 $0$$0$​，有 $(1-p_i)(1-q)$$(1-p_i)(1-q)$​ 的概率变为 $1$$1$​。

对于每个 $x\in [0,2^n)$$x\in[0,2^n)$，求：期望经过多少次操作能首次回到 $x$$x$。

$n\le 20$$n\le 20$​。保证你在计算过程中不需要求 $0$$0$​​​ 的乘法逆。

Part 1 - 随机游走

首先直接写出这个随机游走过程的方程。记 $\mathbf{J}$$\mathbf J$ 是全 $1$$1$ 矩阵，$\mathbf{E}$$\mathbf E$ 是答案向量，$\mathbf{M}$$\mathbf M$ 是转移矩阵，我们有

说人话就是："所有未结束的路径去掉最后一步一定也是未结束的路径；而一条未结束的路径再走一步要么结束要么不结束"。

也即

顺带一提，这里看似只有 $2^{2n}$$2^{2n}$ 个方程，不够解出 $\mathbf{T}$$\mathbf T$ 和 $\mathbf{E}$$\mathbf E$，但应当注意到 $\mathbf{T}$$\mathbf T$ 在主对角线上是 $0$$0$。不过"主对角线上全为 $0$$0$"这个性质还真不太好描述和利用，下面介绍一个方法，它能直接删去 $\mathbf{T}$$\mathbf T$ 这个未知数。（参考资料：《浅谈图模型上的随机游走问题》王修涵）

我们知道，$\mathbf{M}$$\mathbf M$ 这个转移矩阵描述的是一个连通图，由此不难证明 $\mathbf{I}-\mathbf{M}$$\mathbf I-\mathbf M$ 的秩为 $2^n-1$$2^n-1$，也就是说它的核是一个维数为 $1$$1$ 的线性空间。设向量 $\mathbf{X}$$\mathbf X$ 满足

于是

从而，

于是问题变为求 $\mathbf{X}$$\mathbf X$。

Part 2 - 线性代数

也就是 $\mathbf{X}=\mathbf{M}\mathbf{X}$$\mathbf X=\mathbf M\mathbf X$。

然后我们来仔细分析转移矩阵的性质，它应当是

其中 $\otimes$$\otimes$ 表示 Kronecker 积。

如果只有 $\begin{array}{c}\underset{i=0}{\overset{n-1}{⨂}}\left[\begin{array}{cc}1& 0\\ 1-p_i& p_i\end{array}\right]\end{array}$$\bigotimes_{i=0}^{n-1}\begin{bmatrix}1&0\\1-p_i&p_i\end{bmatrix}$​，那么它已经是一个下三角矩阵，我们只需要钦定好 $x_0$$x_0$​ 然后一个一个往回代，和求逆一样做就好了。直接实现是 $O(2^{2n})$$O(2^{2n})$​。

然而我们如果仔细看一眼这个矩阵，就能发现一些有趣的事情：

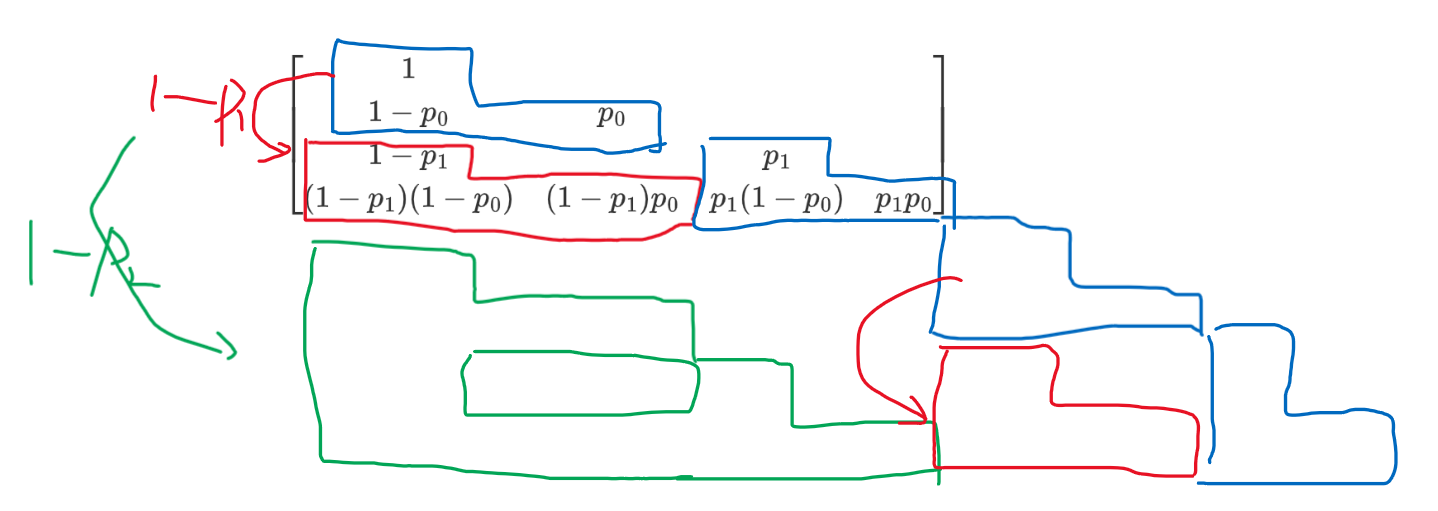
其中蓝色的是首次出现的块，不能从前面的计算中继承；其他的块都是继承来的。可见每行最多被分为 $n$$n$ 块，于是时间复杂度为 $O(n{2}^n)$$O(n2^n)$。

好的，现在回到 $\mathbf{M}$$\mathbf M$​。下面我们来表明，$\mathbf{M}$$\mathbf M$​ 相似于一个与 $\begin{array}{c}\underset{i=0}{\overset{n-1}{⨂}}\left[\begin{array}{cc}1& 0\\ 1-p_i& p_i\end{array}\right]\end{array}$$\bigotimes_{i=0}^{n-1}\begin{bmatrix}1&0\\1-p_i&p_i\end{bmatrix}$​​ 有类似性质的矩阵。

具体来说：我们知道多项式的高次幂问题可以考虑对角化，而 Kronecker 积也是如此。我们有

设 $\begin{array}{c}\mathrm{\Theta }={\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]}^{\otimes n}\end{array}$$\Theta=\begin{bmatrix}1&1\\1&0\end{bmatrix}^{\otimes n}$，从而

记 $\mathbf{M}=\mathrm{\Theta }\cdot \mathbf{L}\cdot {\mathrm{\Theta }}^{-1}$$\mathbf M=\Theta\cdot\mathbf L\cdot\Theta^{-1}$。从而，

于是我们用 $\mathbf{L}$$\mathbf L$ 跑一遍之前的算法就可以得到 ${\mathrm{\Theta }}^{-1}\mathbf{X}$$\Theta^{-1}\mathbf X$，而它和 $\mathbf{X}$$\mathbf X$ 的差别就是一个 FWT。

妈的好像推错了，可能哪里行和列搞反了。被我瞎搞一通后这份代码能过。

​x
#include<bits/stdc++.h>
using namespace std;

const int p = 998244353;
struct Z {int x; Z(int x0 = 0) : x(x0) {}};
int inline check(int x) { return x >= p ? x - p : x; }
Z operator +(const Z a, const Z b) { return check(a.x + b.x); }
Z operator -(const Z a, const Z b) { return check(a.x - b.x + p); }
Z operator -(const Z a) {return check(p - a.x);}
Z operator *(const Z a, const Z b) { return 1LL * a.x * b.x % p; }
Z& operator +=(Z &a, const Z b) { return a = a + b; }
Z& operator -=(Z &a, const Z b) { return a = a - b; }
Z& operator *=(Z &a, const Z b) { return a = a * b; }
Z qpow(Z a, int k) {
    Z ans = 1;
    for (; k; a *= a, k >>= 1) if(k & 1) ans *= a;
    return ans;
}

int n;
Z kq; Z kp[20];

Z x[1 << 20];
Z ans[1 << 20][20];

int main() {
    scanf("%d%d", &n, &kq);
    for (int i = 0; i < n; i++) scanf("%d", &kp[i]);
    for (int s = 0; s < 1 << n; s++) {
        if (s == 0) {
            x[s] = 1;
            for (int i = 0; i < n; i++) ans[s][i] = kq;
            continue;
        }
        Z qaq = 1, sum = 0;
        for (int i = 0; i < n; i++) if ((s >> i) & 1) qaq *= kp[i];
        for (int i = 0; i < n; i++) if ((s >> i) & 1)
            sum += ans[s ^ (1 << i)][i] * (1 - kp[i]);
        x[s] = sum * qpow(1 - qaq, p - 2);
        ans[s][0] += x[s] * kq * qaq;
        for (int i = 0; i < n; i++) {
            if (i) ans[s][i] += ans[s][i - 1];
            if ((s >> i) & 1) ans[s][i] += ans[s ^ (1 << i)][i] * (1 - kp[i]);
        }
    }
    // for (int s = 0; s < 1 << n; s++)
    //     if (s < (((1 << n) - 1) ^ s)) swap(x[s], x[(((1 << n) - 1) ^ s)]);

    for (int i = 0; i < n; i++)
    for (int s = 0; s < 1 << n; s++) if (!((s >> i) & 1)){
        Z a0 = x[s], a1 = x[s | (1 << i)];
        x[s] = a1, x[s | (1 << i)] = a0 - a1;
    }

    Z sx = 0;
    for (int s = 0; s < 1 << n; s++) sx += x[s];
    int ans = 0; Z qaq = 1;
    for (int s = 0; s < 1 << n; s++, qaq *= 2004)
        ans ^= (qaq * sx * qpow(s[x], p - 2)).x;
    printf("%d\n", ans);
}