最近在 uoj 看到了 这篇文章，才终于发现我完全没把半在线 / 在线卷积整明白。

问题. (半在线卷积)

现在有序列 $f$$f$，只有当你得知 $(fg{)}_i$$(fg)_i$ 时才能解密出 $g_{i+1}$$g_{i+1}$。求序列 $g$$g$。

这是一个经典问题。只需要设计如下的分治树（颜色表示计算顺序，每个正方形都是一次卷积）

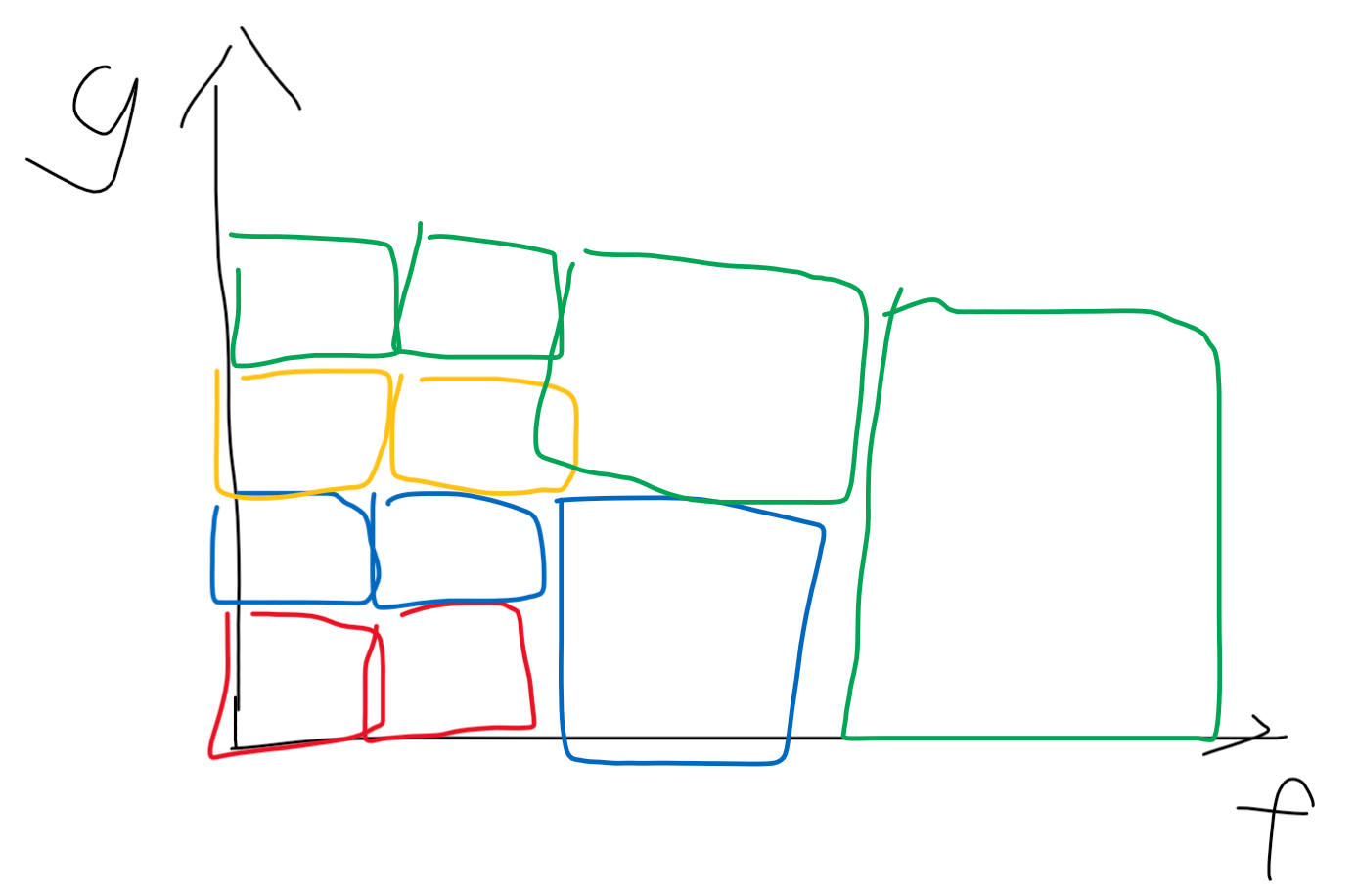
即可。

哎呦这个分治树一画可就比那些阴间递归好多了。

时间复杂度为

当然我们也可以选择多叉：合并时需要技巧，把横轴 $K$$K$ 个多项式和竖轴 $K$$K$ 个多项式分别 DFT，做 $K^2$$K^2$ 次点值乘法，IDFT 时把同相位的多项式合并在一起，只需要做 $2K$$2K$ 次 IDFT。总时间复杂度为

咱也不会分析，实践上取 $K=\log n$$K=\log n$ 即可。

现在我们来考虑一个新问题：

问题. (全在线卷积)

你已经知道 $f_0,g_0$$f_0,g_0$，只有当你得知 $(fg{)}_i$$(fg)_i$ 时才能解密出 $f_{i+1},g_{i+1}$$f_{i+1},g_{i+1}$。求序列 $f,g$$f,g$。

我们指出全在线卷积问题可以规约为半在线卷积问题。

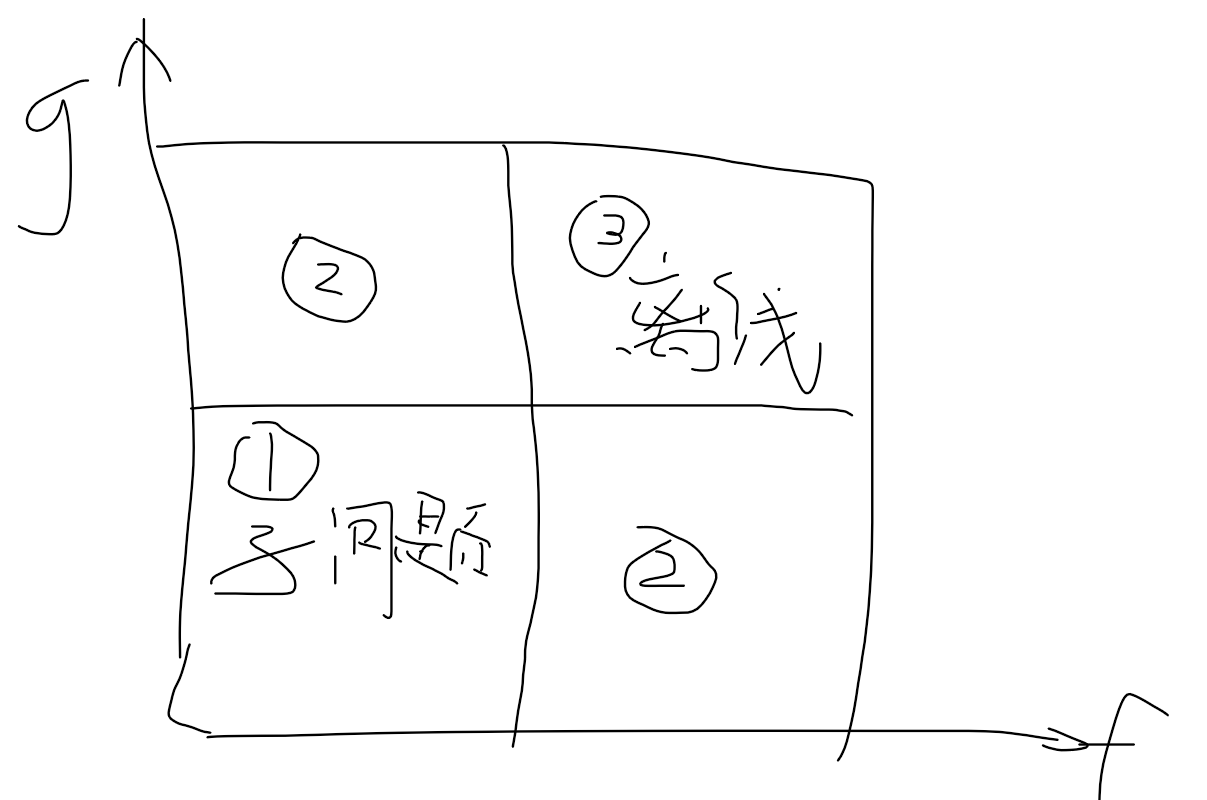
我们按 ① -> ② -> ③ 的顺序求解。① 是一个子问题，③ 在 ② 求解完毕后就是一个离线卷积。现在来关注 ②。不难发现 ② 实际上就是两个需要协调的半在线卷积问题：

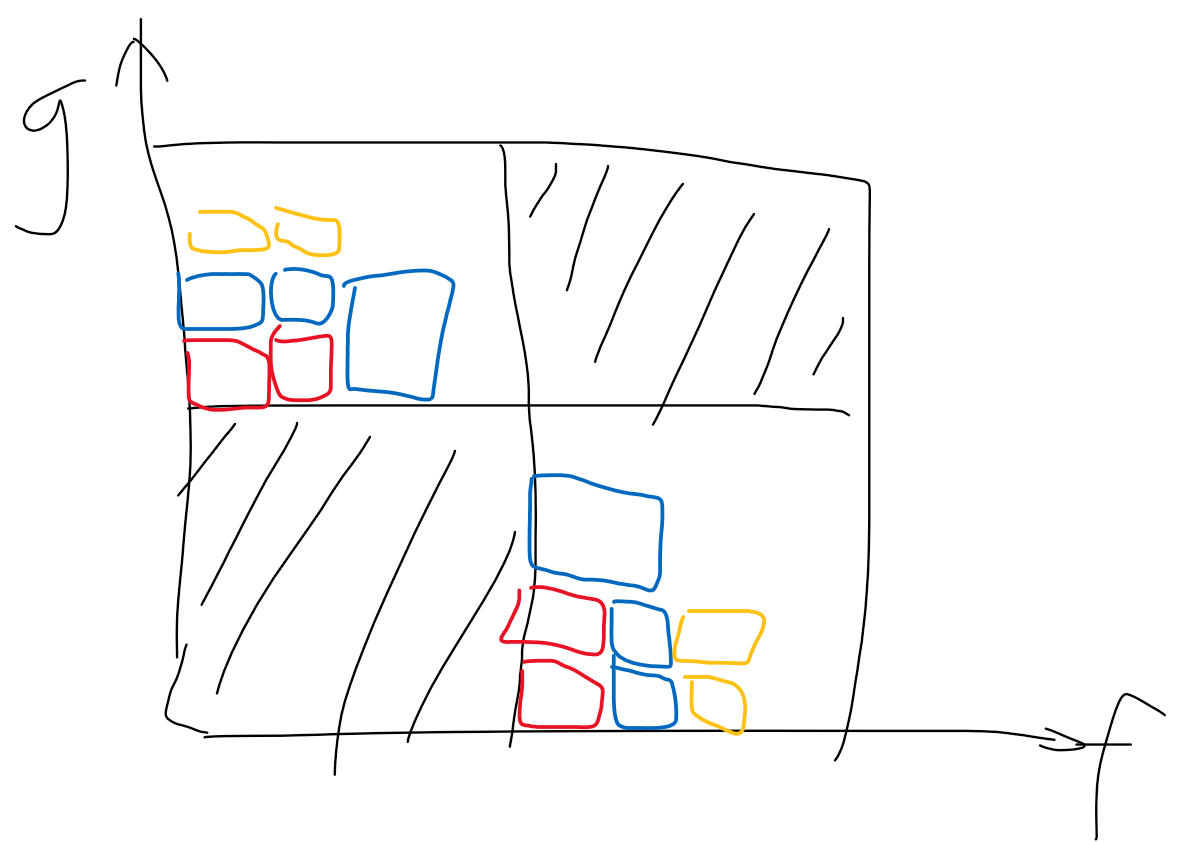
经计算，全在线卷积的时间复杂度与半在线卷积相等。