一个广义串并联图可以用数次以下操作被缩为一个点：

• 删 $1$$1$ 度点。
• 缩 $2$$2$ 度点。
• 叠合重边。

判定一个图是不是广义串并联图很简单，如果你发现它的边不是很密集那么它大概率就是一个广义串并联图，比如一个加了一条边的仙人掌（[SNOI2020] 生成树）：

题目大意.

给出一个加了一条边的仙人掌。求其生成树个数。

$n,m\le 5\text{e}5$$n, m\le 5\text{e}5$。

好的！我们直接来维护整体的生成树个数。

• 删 $1$$1$ 度点：不影响生成树个数。
• 缩 $2$$2$ 度点：……

我们遇到了很大的困难（悲）。关键在于：与 $2$$2$ 度点相连的两条边不能同时存在，这免不了把三种情况分开讨论。而我们甚至没法把它们分离出来。

考虑 TopTree 的结构，我们来维护每个簇内的生成树个数。每个簇对外表现为一条链接两个点的边，但是实际上它存在一个神必的隐藏结构，我们就是要额外维护这个隐藏结构的生成树个数。

回头考虑缩 $2$$2$ 度点。图中隐藏掉的两条边和一个点就是簇的隐藏结构。

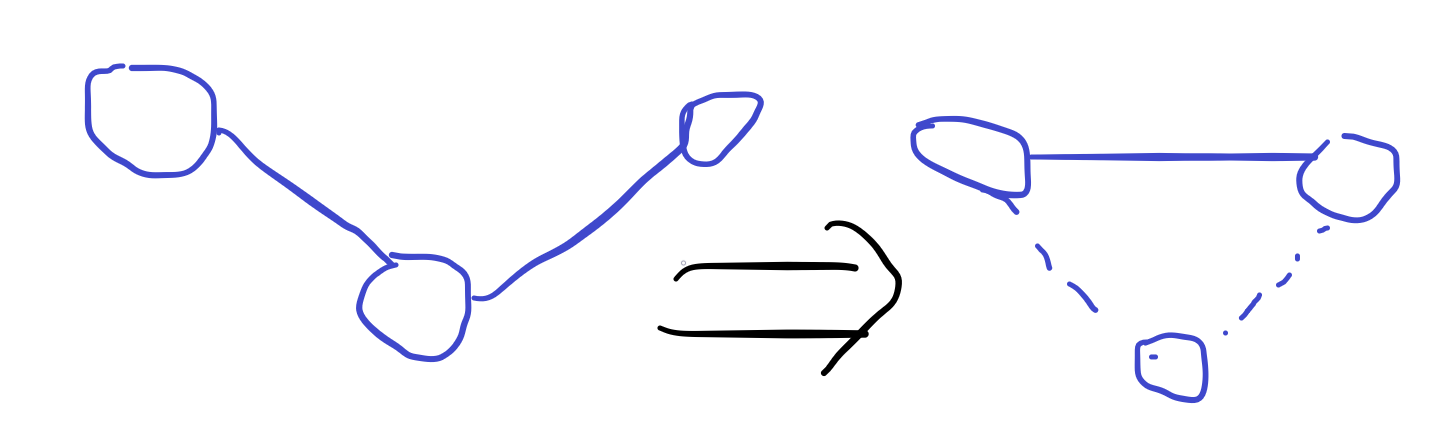
那么，上图的结构什么时候会表现为“这条边表现得像被选了”呢？当且仅当隐藏的两条边都被选了。那么表现为“这条边表现得像没被选”当且仅当隐藏的两条边恰选了一条。

另外还可见“对外边”的被选与否会影响到隐藏结构，于是我们记 $f_e$$f_e$ 为 $e$$e$ 被选时，隐藏结构组织为生成树的方案数，$g_e$$g_e$ 反之。上述讨论总结为

• 叠合重边：

容易分析得到

• 回头看看删 $1$$1$ 度点：

可见这个簇直接消失了，事实上它体现出的是：最终，其他边任意，而这个簇必选。其实就是答案 *= $f_e$$f_e$ 的意思。

​x
#include<bits/stdc++.h>
using namespace std;

const int p = 998244353;

int n, m;

struct Edge {
    int f, g;
};
map<int, Edge> G[500005];

set<int> Q[2]; int lstdeg[500005];
void upd_deg(int x) {
    if (lstdeg[x] <= 2 && lstdeg[x]) Q[lstdeg[x] - 1].erase(x);
    if (G[x].size() <= 2 && G[x].size()) Q[G[x].size() - 1].insert(x);
    lstdeg[x] = G[x].size();
}
void del_edge(int u, int v) { G[u].erase(v); G[v].erase(u); }
void ins_edge(int u, int v, Edge w) {
    if (G[u].count(v)) {
        Edge w0 = G[u][v];
        G[u][v] = G[v][u] = (Edge){(1LL * w.f * w0.g + 1LL * w.g * w0.f) % p, 1LL * w.g * w0.g % p};
    }
    else G[u][v] = G[v][u] = w;
}

int main() {
    scanf("%d%d", &n, &m);
    while(m--) {
        int u, v; scanf("%d%d", &u, &v);
        ins_edge(u, v, (Edge){1, 1});
    }
    for (int i = 1; i <= n; i++) upd_deg(i);
    int ans = 1;
    while(Q[0].size() || Q[1].size()) {
        if (Q[0].size()) {
            int u = *Q[0].begin();
            int v = G[u].begin() -> first;
//          printf("del 1 deg : %d %d\n", u, v);
            ans = 1LL * ans * G[u][v].f % p;
            del_edge(u, v); upd_deg(u); upd_deg(v);
        }
        else {
            int u = *Q[1].begin();
            map<int, Edge>::iterator i = G[u].begin();
            int v1 = i -> first; int v2 = (++i) -> first;
//          printf("del 2 deg : %d %d %d\n", u, v1, v2);
            Edge w1 = G[u][v1], w2 = G[u][v2];
            ins_edge(v1, v2, (Edge){1LL * w1.f * w2.f % p, (1LL * w1.f * w2.g + 1LL * w1.g * w2.f) % p});
            del_edge(u, v1); del_edge(u, v2);
            upd_deg(u); upd_deg(v1); upd_deg(v2);
        }
    }
    printf("%d\n", ans);
}