参考资料：论文集2019《浅谈杨氏矩阵在信息学竞赛中的应用》袁方舟，《对称群笔记》Wenchao Zhang。

引入

杨图，杨表，勾长公式

杨图（记为 $\lambda$）大概就是一个长成这样的东西：

每行的列数称为 $\lambda_1,\lambda_2,...\lambda_m$。$\lambda_i$ 单调不增，和为 $n$，称为 $\lambda\vdash n$。

你要往里面填 $1...|\lambda|$ 的排列，使得行单调增列单调增，这样的一种填充称为标准杨表。杨表数量由下面的勾长公式给出。

设 $\text{hook}(p)$ 是杨图中格子 $p$ 的勾长，等于其下方格子个数+右方格子个数+1。

标准杨表总数为

$$f_{\lambda}=\dfrac{|\lambda|!}{\prod_{p\in \lambda}\text{hook}(p)}$$

也可以完全只用 $\lambda$ 表达：

$$f_{\lambda}=n!\dfrac{\prod_{i<j}(\lambda_i-i-\lambda_j+j)}{\prod_{i=1}^m(\lambda+m-i)!}$$

半标准杨表，勾长公式

即行不严格递增，列严格递增的杨表。

设值域为 $r$，半标准杨表数为

$$\prod_{p\in\lambda}\dfrac{r+p_y-p_x}{\text{hook}(p)}$$

斜杨图

即从一个杨图 $\lambda$ 中扣掉另一个杨图 $\mu$。不连通也没关系。

一个兴奋图（写出这个东西的英文名可能导致寿命减少）是指，$\mu$ 经过一系列的兴奋运动形成的 $\lambda$ 的某个子集。对 $\mu$ 的兴奋运动是指，将一个下方右方右下方都属于 $\lambda/\mu$ 的属于 $\mu$ 的方格移动到其右下方。

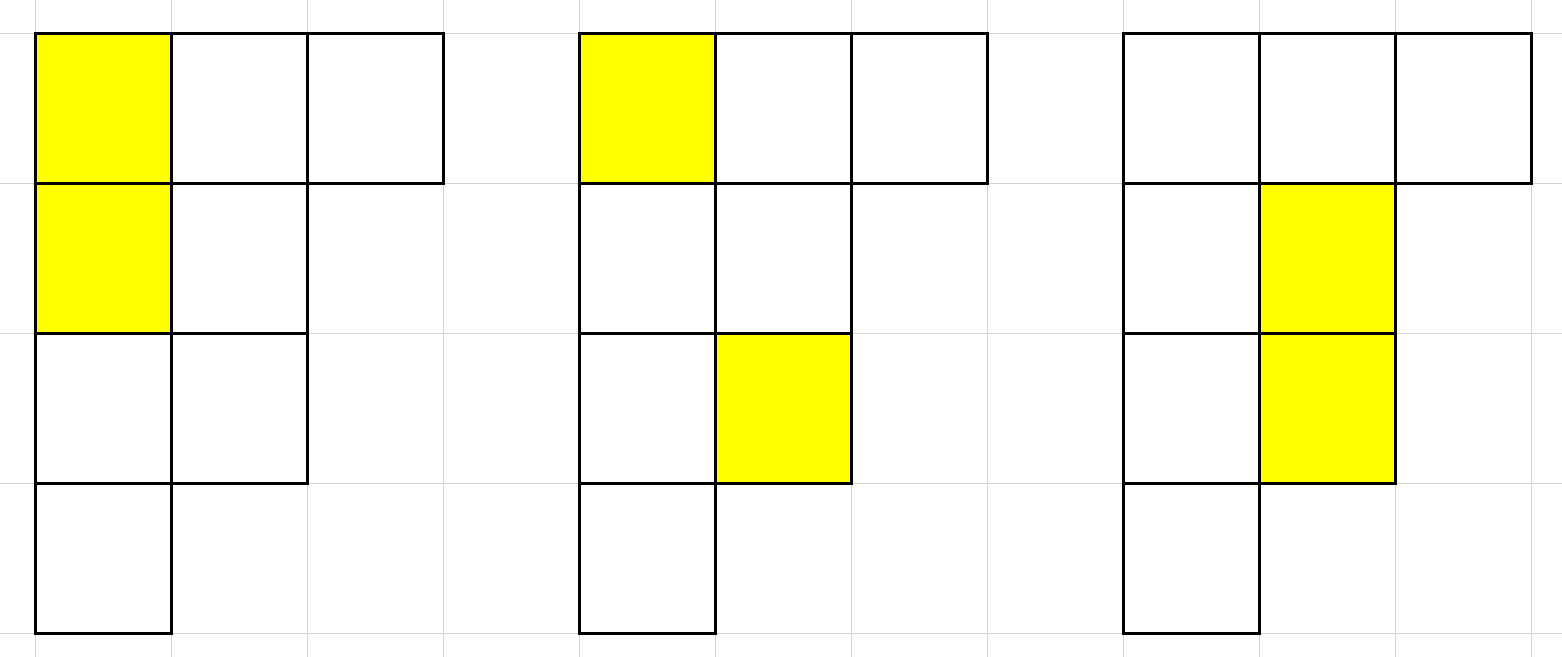
如图是 $\mu$ 的所有可能的兴奋图。记为 $\mathcal{E}(\lambda/\mu)$。如下是勾长公式。

$$|\lambda/\mu|!\sum_{D\in\mathcal E{(\lambda/\mu)}}\prod_{p\in \lambda/D}\dfrac{1}{\text{hook}_{\lambda}(p)}$$

RSK 算法，杨表与 LIS 问题

下面我们将揭示杨图和排列的深刻联系。先引入 $\text{RSK}$ 算法。

RSK 算法

行插入

定义 $P\leftarrow x$ 是把 $x$ 从第一行行插入进近似标准杨表（即填入的元素不必是 $1...|\lambda|$）$P$ 中。流程如下：

• 找到本行最小的比 $x$ 大的数 $y$。如果找不到这样的 $y$，则把 $x$ 放在本行末尾并结束算法。
• 交换 $x,y$。将 $y$ 行插入下一行。

如下演示了一个行插入过程。

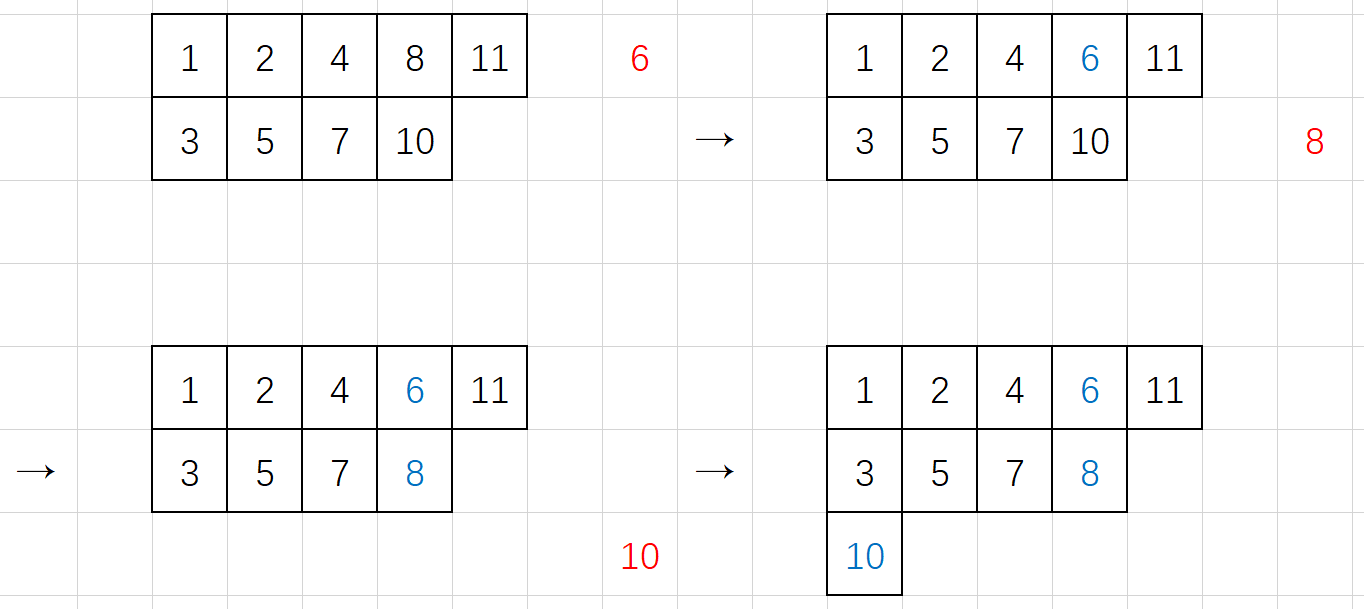
显然最后新增的格子一定在边角，即其下方和右方都没有格子。

对于对 $P$ 的第 $i$ 插入，在另一个杨表 $Q$ 中在新增的格子上写上 $i$（注意不是插入）。显然 $Q$ 是标准杨表。我们称 $P$ 为插入表，$Q$ 为记录表。

删除

下面定义从 $P$ 中删除格子 $p$。尽管看起来不必要，我们还是规定 $p$ 必须是边角。记 $p$ 中填的数是 $x$。流程如下：

• 如果这是第一行，结束算法。
• 找到上一行最大的比 $x$ 小的数 $y$（显然一定存在）
• 交换 $x,y$，移到上一行继续算法。

结束算法后删掉已经没有数的格子 $p$。

如下演示了一个删除过程。

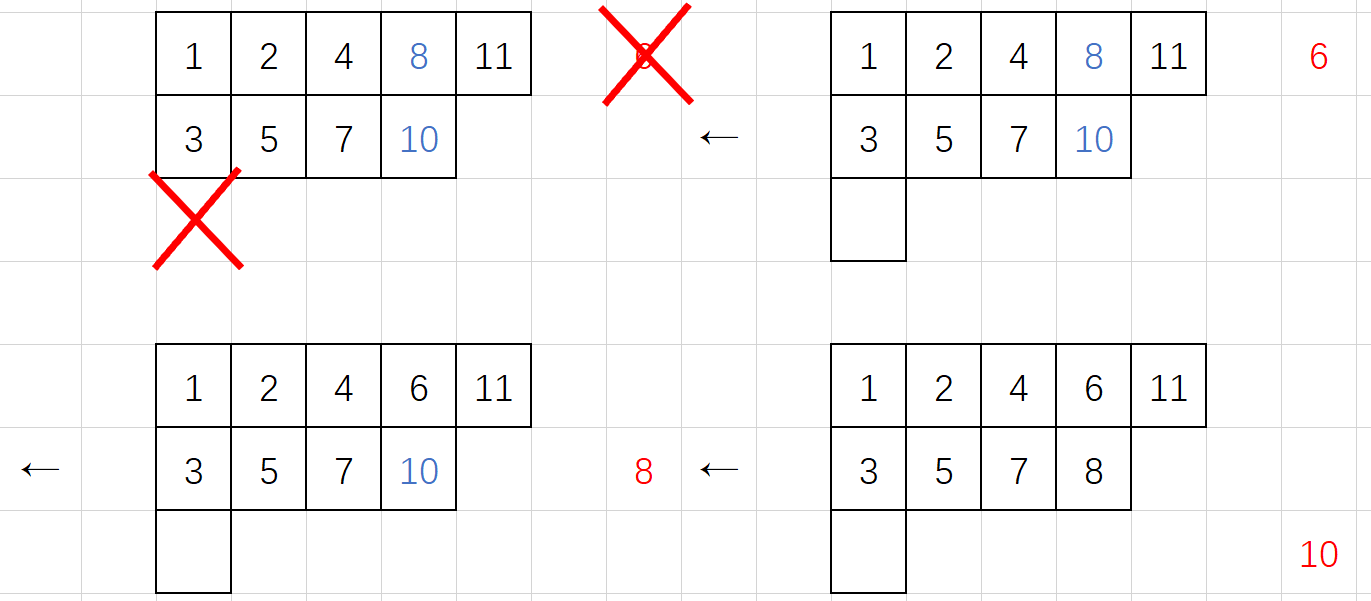
很明显删除就是行插入的逆操作。

考虑一个 $1...n$ 的排列，依次插入即可得到两个杨表 $(P,Q)$；给定 $(P,Q)$，显然 $Q$ 中最大元素一定在边角，于是我们可以按 $Q$ 的指导去删除 $P$ 来还原原来的排列。

于是也就得到了以下的Robinson–Schensted correspondence：

上述算法构成了 $(P,Q)$ 到 $S_n$ 的一一映射。也就是说，

$$\sum_{\lambda\vdash n}f_{\lambda}^2=n!$$

不禁让人联想到 prüfer 序列。

同时对于置换（当然也是排列）$\pi\rightarrow (P,Q)$，我们有 $\pi^{-1}\rightarrow(Q,P)$，从而每一个标准杨表 $P$ 对应一个对合，即逆等于自身的置换。对对合计数，我们得到：

$$\sum_{\lambda\vdash n}f_{\lambda}=\sum_{k=0}^{\lfloor n/2\rfloor}{n\choose 2k}(2k-1)!!$$

其中双阶乘 $(2k-1)!!$ 定义为 $(2k-1)(2k-3)...3\cdot 1$。

RSK 算法和半标准杨表

一个广义置换大概可以理解为可重集上的置换，比如

它对应一个广义置换矩阵，这个矩阵的第 $i$ 行 $j$ 列表示 $i$ 到 $j$ 的个数。

我们有

一个广义置换和一个半标准杨表对一一对应。具体来讲就是运行 RSK 算法，把第二行的元素插入 $P$，$Q$ 中记录第一行的元素。

而如果有广义置换矩阵 $M\rightarrow(P,Q)$，则 $M^T\rightarrow(Q,P)$。

杨表和 LIS 问题

LIS 即最长上升子序列，LDS 即最长下降子序列。

显然有如下结论：

• 杨表第一行的长度即 $s$ 的 LIS 的长度。但是第一行并非 $s$ 的 LIS。
• 若有 $s\rightarrow(P,Q)$，则 $s$ 的翻转 $\text{rev}(s)\rightarrow(P^T,Q')$。其中 $P^T$ 是 $P$ 的转置，$Q'$ 和 $Q$ 没什么关系。
• 于是我们得到杨表第一列的长度即 $s$ 的 LDS 的长度。

「CTSC2017」最长上升子序列

根据 Dilworth 定理，一个序列的 LIS 的长度等于将其分为若干个不上升子序列所需数量的最小值。那么最长的 $C$ 就是 $B$ 对应的“$\le$ 杨表”的前 $k$ 行长度之和。

不幸的是直接暴力实现杨表插入是 $n^2\log n$ 的。考虑根号分治，分别维护前 $\sqrt n$ 行和前 $\sqrt n$ 列。对于前 $k$ 列，它就是对应的“$>$ 杨表”（标准杨表）的前 $k$ 行。

明明和杨表没有深入关系，但是不会杨表就做不了的屑题

[BJWC2018]最长上升子序列

爆枚杨表形态即可。整数拆分 $p(n)$ 渐进意义上等于

顺瑇一提这个公式是拉马努金发现的（

杨表和网格图路径数

记 $P(\mathcal A\rightarrow\mathcal E)$ 是点 $\mathcal A$ 到点 $\mathcal E$ 的路线的集合，每一步只能往右边走或者往上方走。两条路径相交即有公共点。显然 $|P(\mathcal{A\rightarrow E})|={E_1+E_2-A_1-A_2\choose E_1-A_1}$。

卡塔兰数

卡塔兰数的组合意义即从 $(0,0)$ 走到 $(n,n)$，任何时刻横坐标不能小于纵坐标。考虑 $X_i$ 为横坐标到达 $i$ 的时间，$Y_i$ 亦然，那么它就对应如下的一个杨表。

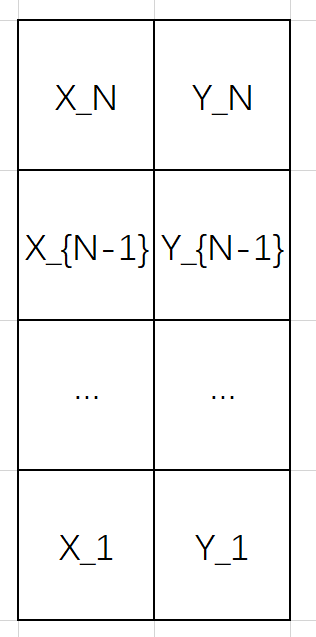
显然一个 $2\times n$ 的标准杨表和路径一一对应。从而 $2\times n$ 的标准杨表数即卡塔兰数。

「雅礼集训 2017 Day11」PATH

显然题目要求的路径对应一个 $\{a_1,a_2,...,a_n\}$ 的杨表。式子化出来是

FFT 统计有多少对 $(i,j)$ 满足 $a_i-i-a_j+j=k$，然后就好了。

LGV 引理

给出平面上的 $n$ 个点对 $(\mathcal A_i,\mathcal E_i)$，记 $P_i=P(\mathcal A_i\rightarrow \mathcal E_i)$。则从 $P_1,P_2,...,P_n$ 中各取一条路径，使得它们互不相交的方案数为

$$\text{det}\left|\ |P(\mathcal A_i\rightarrow E_j)\right|\ |$$

事实上该引理适用于所有有向无环图。

考虑容斥掉所有存在相交的方案。对于一个相交的方案，我们找到一个最大（这个最大可以任意定义，只要唯一即可）的相交点，则我们可以交换相交后的这条路径。

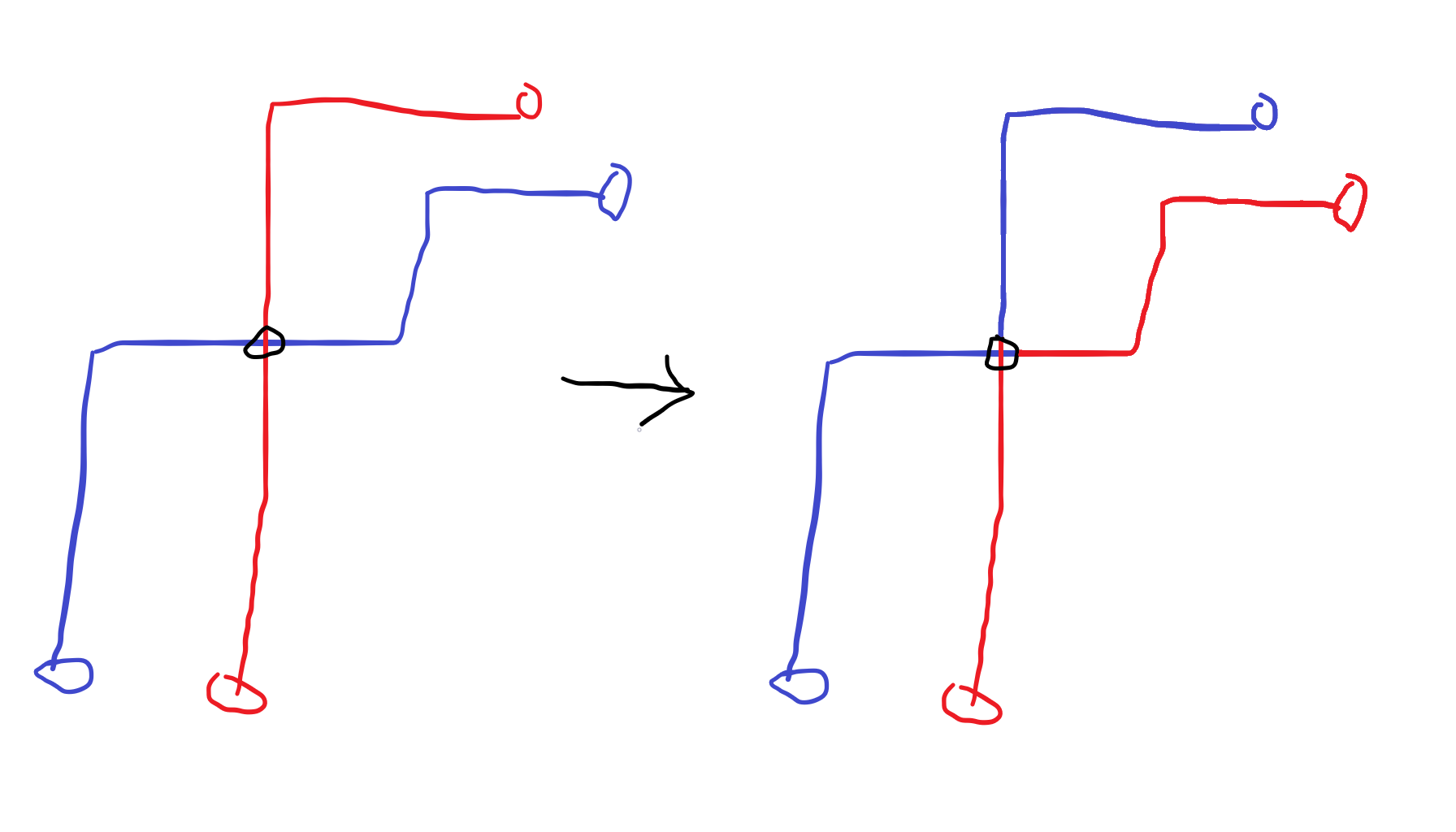
为了让它们相互抵消，交换后容斥系数应当乘以 -1。我们发现这正是置换的符号 $\text{sgn}(\sigma)$ 的定义。（-1 的逆序对个数次方）写出式子：

这正是行列式的定义。

和卡塔兰数类似，不相交路径集合也和杨表有对应。

一个元素在 $[1,n]$ 的半标准斜杨表 $\lambda/\mu$ 和一个 $\mathcal A_i=(\mu_i-i,1),\mathcal E_i=(\lambda_i-i,n)$ 的不相交路径集合对应。

比较显然。

k-Dyck Path

1-Dyck Path 就是卡塔兰路径。k-Dyck Path 是 $k$ 条卡塔兰路径，但第二条必须完全在第一条“内部”，第三条必须完全在第二条内部……

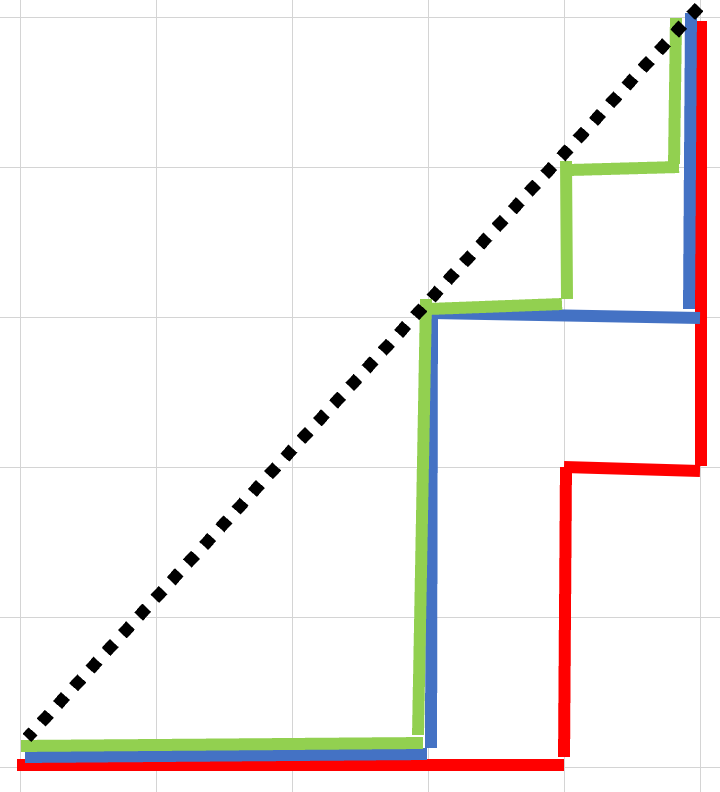
一元素在 $[1,n]$ 的 $\lambda_i$ 均为偶数的半标准杨表和 $n+1$ 阶的 k-Dyck Path 对应，且公式如下

$$b_{n,k}=\prod_{1\le i\le j\le n}\dfrac{2k+i+j}{i+j}$$

记录下每条 Dyck_Path 的由上方向转为右方向的拐角即可证明。

后记

完结撒花。

因为我学不动了。